Quicksort, Insertion Sort and Radix Sort Comparison
Complexity of an algorithm is determined as consumed resources like time and space. It depends not only on the number of input elements but also on their order. In this work, I tried to demonstrate how order of inputs affects the time complexity for different sorting algorithms. In particular, I experimented with quicksort, insertion sort and radix sort. Here are Big-O time complexities of these sorting algorithms:
| Algorithm | Worst case | Best case | Average case |
|---|---|---|---|
| Quicksort | \(O(n^2)\) | \(O(n\log{}n)\) | \(O(n\log{}n)\) |
| Insertion sort | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) |
| Radix sort | \(O(kN)\) | \(O(kN)\) | \(O(kN)\) |
In this experiment, the input is a pair of number and word. First, the file will be read and then numbers will be sorted in descending order with each sorting algorithm. Here is how the input looks like:
1000 to
999 dedicated
998 here
997 be
996 to
995 us
994 for
993 rather
...In order to test boundary cases for different input orders, three different input versions are used:
- data1.txt: already sorted in ascending order
- data2.txt: random order (sorted by word)
- data3.txt: already sorted in descending order
Here are average runtime for each file and algorithm:
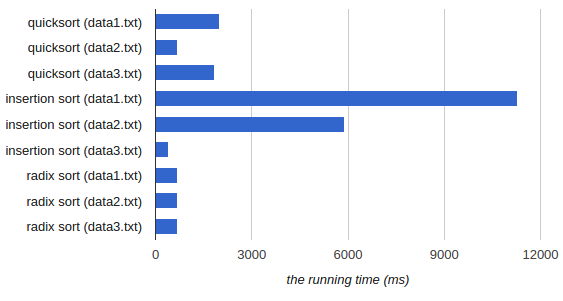
| Algorithm | data1.txt | data2.txt | data3.txt |
|---|---|---|---|
| Quicksort | 1980 ms | 680 ms | 1840 ms |
| Insertion Sort | 11270 ms | 5890 ms | 400 ms |
| Radix Sort | 680 ms | 690 ms | 690 ms |
Based on the result:
- Quicksort: Already sorted and reverse sorted inputs are the worst cases.
data2.txthas the best run-time for three inputs because it is random. - Insertion Sort: The best case is the already sorted input and the worst case is the already reverse sorted input.
In this experiment, the task is to sort the numbers in descending so
data3.txtis the best case anddata1.txtis the worst case. - Radix Sort:: The run-times are almost the same for all inputs because radix sort’s performance is independent from input order. Thus, linearly sorted inputs are not worst or best case for insertion sort.
This experiment shows that, order of the input is important as input size. Although size of inputs are the same, the order changes the runtime dramatically.
Here is the code in C++:
References
- Cormen, Thomas H. Introduction to algorithms. MIT press, 2009.
